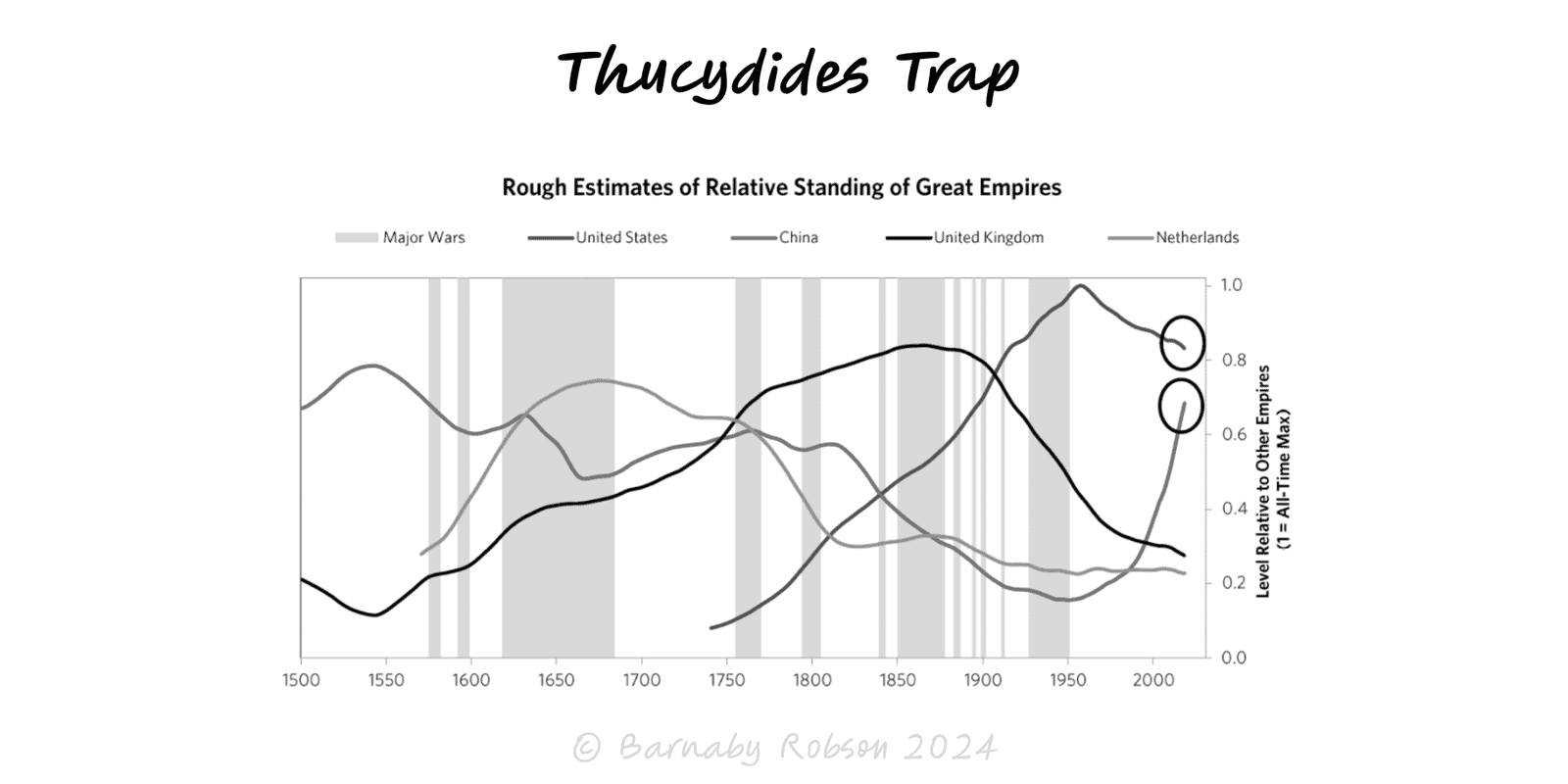
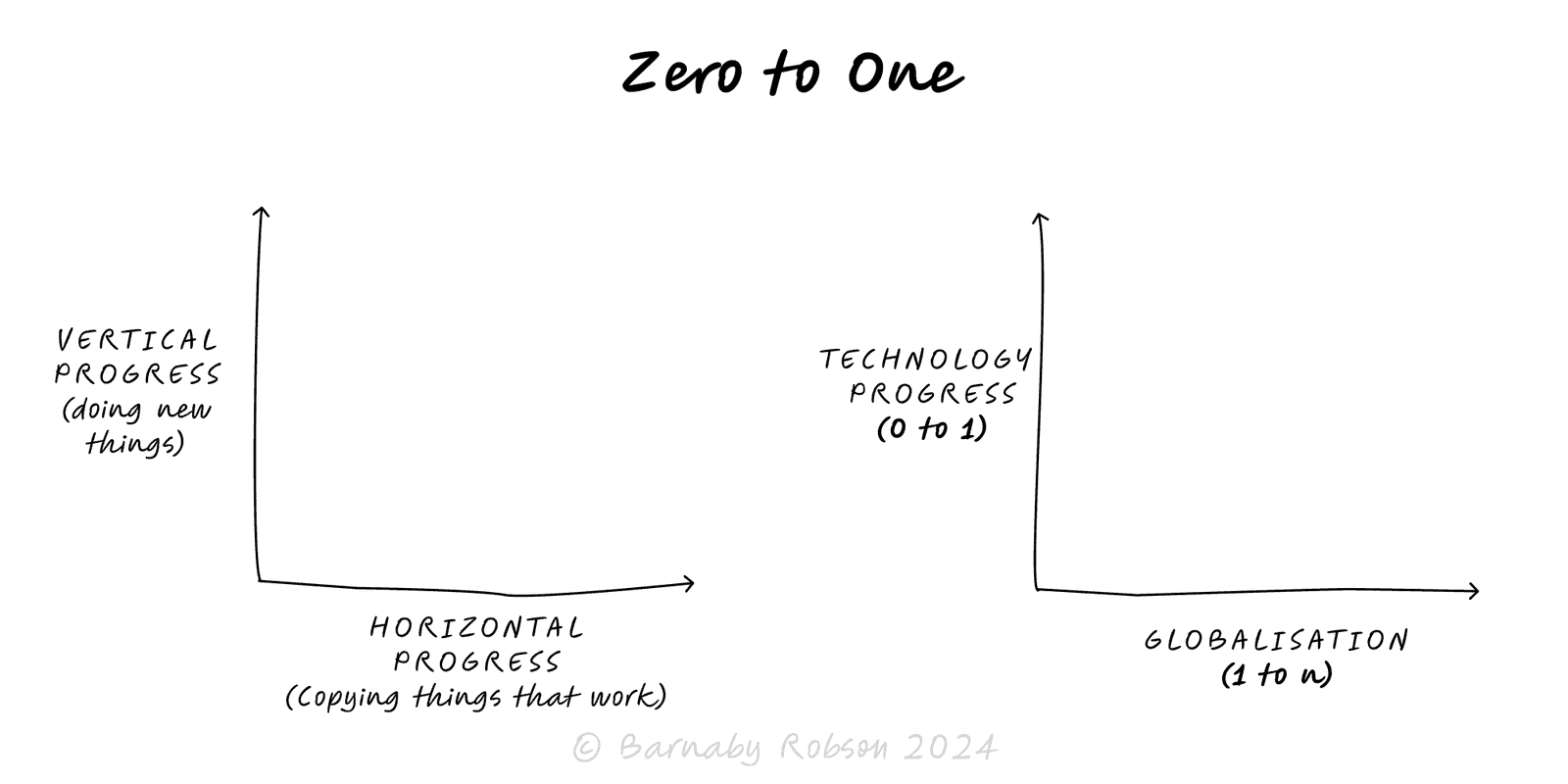
Chaos Dynamics
Sensitivity to initial conditions and non‑linear feedbacks can make long‑range prediction impossible; manage by bounds, not points.
Author
Henri Poincaré (foundations), Edward Lorenz (weather “butterfly effect”), Robert May (logistic map) — modern systems thinking
Model type