Combinations vs Permutations
Order matters → permutations. Order doesn’t → combinations. Adjust for with/without replacement.
Author
Classical combinatorics (Pascal, Newton and successors)
Model type
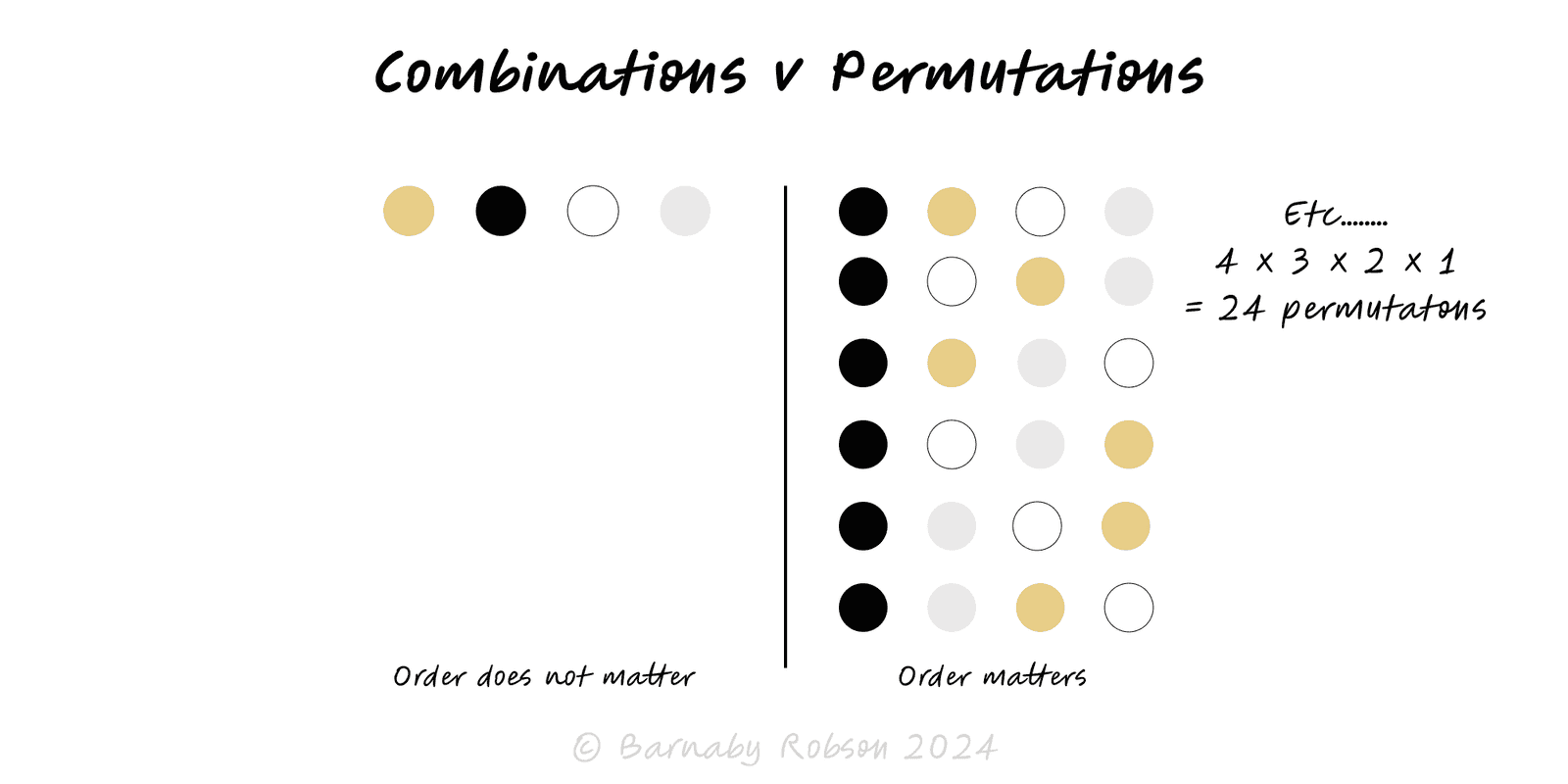
Order matters → permutations. Order doesn’t → combinations. Adjust for with/without replacement.
Classical combinatorics (Pascal, Newton and successors)

Counting outcomes underpins probability, testing and design choices. Permutations count ordered selections; combinations count unordered selections. The right choice depends on two questions: (1) does order matter? (2) can you reuse items (replacement)? Getting this right prevents over/under-counting, bogus probabilities and wrong sample sizes.
Notation & basics
The four common cases
| Order matters? | Replacement? | Count | |
|---|---|---|---|
| 1 | Yes | No | P(n,r) = n!/(n−r)! |
| 2 | Yes | Yes | n^r |
| 3 | No | No | C(n,r) = n!/[r!(n−r)!] |
| 4 | No | Yes | C(n+r−1, r) (combinations with repetition) |
Quick intuition
Product & ops – SKU/option explosion, menu design, routing/scheduling possibilities.
Research & testing – number of test variants, multi-factor designs, sample-space sizing.
Security – password/PIN complexity, keyspace sizing.
Hiring & teams – ways to assign roles, select panels or rota patterns.
Risk & probability – lottery odds, card draws, defect sampling (hypergeometric vs binomial).
Define items and r – “Choose r from n”. State any caps or must-include rules.
Decide order – does arrangement change meaning? If yes, use permutations.
Decide replacement – can an item repeat? If yes, use the replacement versions.
Write the formula – pick from the 4-case table; simplify algebraically.
Sanity-check – test extremes (r = 0, r = 1, r = n) and small n with manual enumeration.
Add constraints – if there are exclusions (e.g., “at least one vowel”), use inclusion–exclusion or break into cases.
For large n – use log-factorials / Stirling’s approximation to avoid overflow; or simulate to validate.
Worked mini-examples<
Team selection: choose 3 judges from 10. Order doesn’t matter, no replacement → C(10,3) = 120.
Podium outcomes: gold–silver–bronze from 10. Order matters, no replacement → P(10,3) = 720.
3-digit PIN: digits 0–9, order matters, replacement allowed → 10³ = 1000.
Scoops with repeats: 3 scoops chosen from 5 flavours, order irrelevant, repeats allowed → C(5+3−1,3) = C(7,3) = 35.
Dividing (or not) by r! incorrectly – causes ×r! errors.
Forgetting replacement rules – using n^r when items can’t repeat, or P/C when they can.
Hidden constraints – “no adjacent duplicates”, “at least one from X” change the count.
Indistinguishable items – identical objects require stars-and-bars or partition methods, not plain P/C.
Over-relying on averages – probability conclusions fail if the sample space was miscounted.
Click below to learn other mental models

Before building, map the space: the key forks, dead ends and dependencies—so you can choose a promising path and run smarter tests.
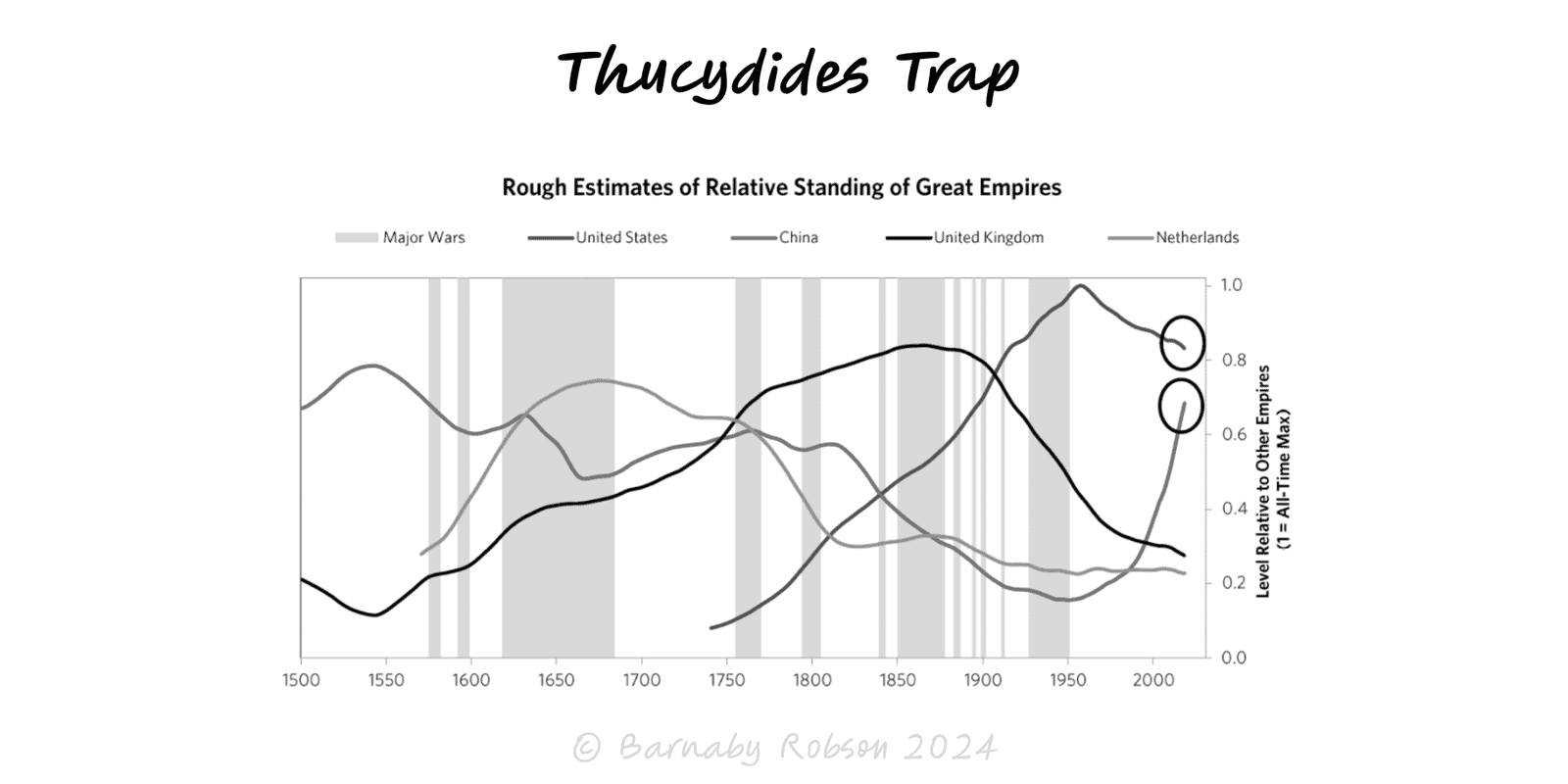
When a rising power threatens to displace a ruling power, fear and miscalculation can tip competition into conflict unless incentives and guardrails are redesigned.
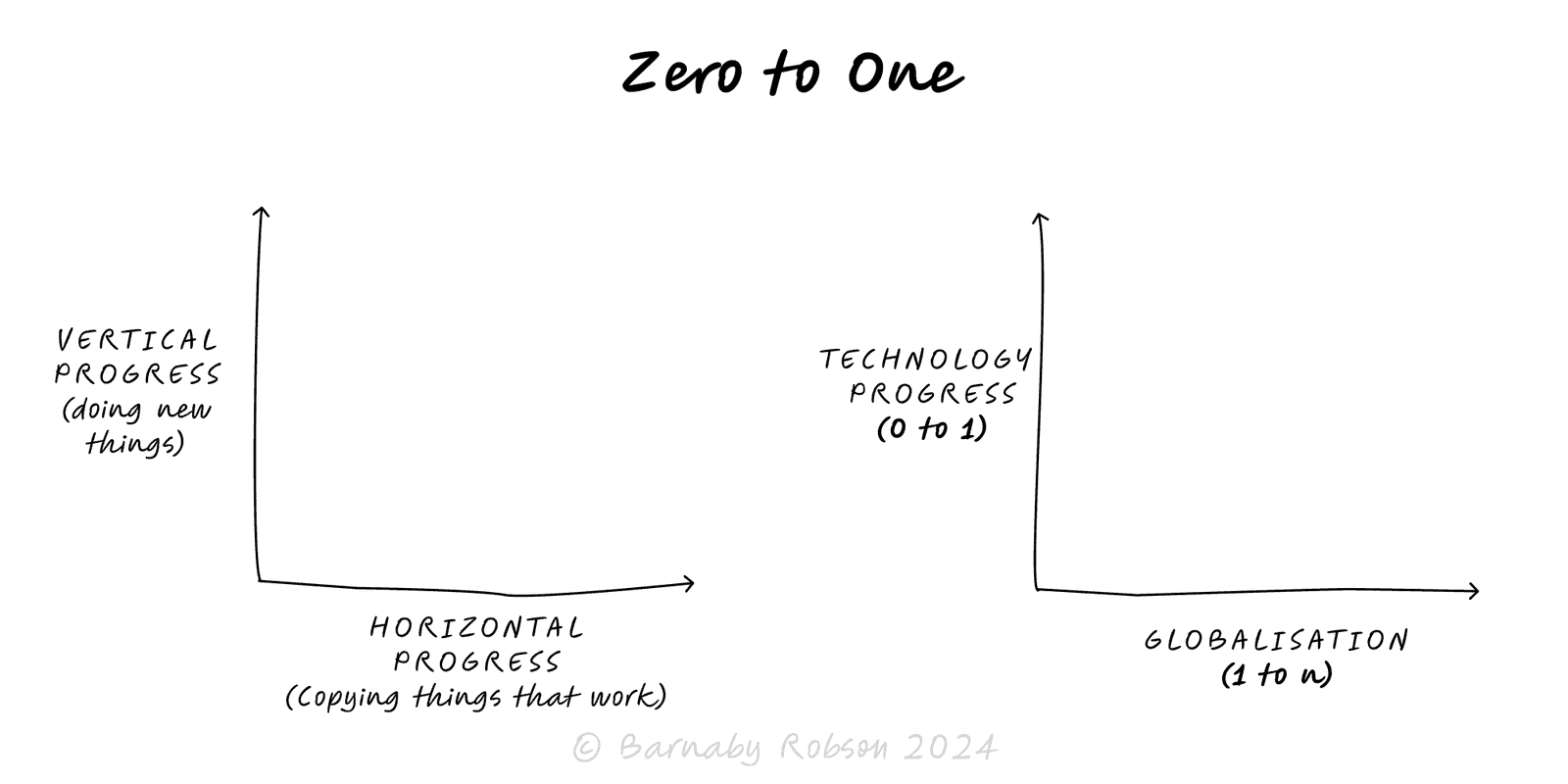
Aim for vertical progress—create something truly new (0 → 1), not just more of the same (1 → n). Win by building a monopoly on a focused niche and compounding from there.